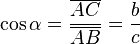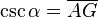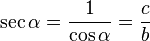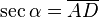Para el examen!!!!

Chicos no olviden que el examen se acerca aqui están las fórmulas:

Cubo:

Si a es la arista de un cubo, entonces:

Área = 6a²
Volumen = a³      

Paralelepípedo:

Si a, b y c son los lados de un paralelepípedo, entonces:

Área = 2ab + 2ac + 2bc
Volumen = abc

Cilindro:

Si r es el radio basal y h es la altura del prisma, entonces:

Área basal = 2π²
Área lateral = 2πh
Área total = 2²π + 2πh
Volumen = V = π²h

Cono recto:

Si r es el radio basal, h la altura y g la generatriz del cono, entonces:
Área basal = πr²
Área lateral = πr g
Área total = πr (g+r)
Volumen = 1/3πr^{2 h}

Esfera:

Área de la esfera = 4 x π
El volumen de la esfera = 4/3 x π x r3





Marina Cieza Abarca Nº 6 4º E

 x r2

Trigonometría:)

¿QUÉ ES?

La trigonometría es una rama de la matemática, cuyo significado etimológico es "la medición de los triángulos".

La trigonometría es la rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos. Para esto se vale de las razones trigonométricas, las cuales son utilizadas frecuentemente en cálculos técnicos.

En términos generales, la trigonometría es el estudio de las funciones seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.

Posee numerosas aplicaciones: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas de navegación por satélites.

RAZONES TRIGONOMÉTRICAS:

• El seno (abreviado como sen, o sin por llamarse "senos" en latín) es la razón entre el cateto opuesto sobre la hipotenusa,

• El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa,

• La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente,

• La Cosecante: (abreviado como csc o cosec) es la razón recíproca de seno, o también su inverso multiplicativo:

En el esquema su representación geométrica es:

• La Secante: (abreviado como sec) es la razón recíproca de coseno, o también su inverso multiplicativo:

En el esquema su representación geométrica es:

• La Cotangente: (abreviado como cot o cta) es la razón recíproca de la tangente, o también su inverso multiplicativo:

Marina Cieza 4e Nº 6

Simbolos matemáticos :O

El origen de los símbolos matemáticos.

- El matemático alemán Michael Stifel en su obra Arithmetica Integra popularizó los símbolos “+” y “-” desplazando a los signos “p” (plus) y “m” (minus).
- Robert Recode, matemático y médico inglés, fue el creador del símbolo “=“. Para él no había dos cosas más iguales que dos lineas rectas paralelas.

- El símbolo que conocemos como “raíz de” apareció por primera vez en un libro alemán de álgebra de 1525. Antes, para designar la raíz de un número se escribía literalmente “raíz de”. Para abreviar se usó simplemente la letra “r“, pero cuando los números eran grandes se alargaba el trazo horizontal de la misma dando origen al símbolo que utilizamos hoy en día.
- El matemático François Viète fue el primero en utilizar letras para designar las incógnitas y constantes.

- A Tomas Harriot le debemos los signos actuales de “>” y “<“, y el “.” como símbolo de multiplicación.
- Los símbolos de multiplicación “x” y división “:” fueron introducidos por el matemático William Oughtred en el año 1657.

- El símbolo de la integral fue propuesto por Gottfried Leibniz y lo extrajo de la palabra latina “summa” tomando su inicial. A Leibniz le debemos muchos más signos notacionales como “dx” y además fue quien popularizó el “.” como signo de multiplicación.


Hola!! A mi parece algo sumamene interesante, de lo cual jamás me habian hablado, y supongo que al fin y al cabo lo sobreentendemos sin preguntarnos por que... ojala les guste:D esta realmante interesante:D:D
Carolina López Ezaine 4to"E

Fotos --> Conos truncados:D:D

IMÁGENES DEL CONO TRUNCADO EN LA VIDA COTIDIANA

Aquí les muestro algunas imágenes que encontré, las cuales tienen forma de cono truncado.

ESPERO QUE LES GUSTE!!  :)

Comentario:

No creí poder encontrar tantas imágenes del cono truncado en nuestra vida cotidiana.

Es Increíble que podamos encontrar desde inmensas construcciones, hasta postres con esta  forma.

Ana Lucía Vargas 4to"E"

VIDEOO:D

Frescia Dominguez 4to"E"

CalculaDora!!:D:D

Evolución  de la calculadora

Origen: el ábaco

Construidos a menudo como un marco de madera con cuentas deslizantes sobre alambres. Los ábacos fueron usados durante siglos antes de la adopción del sistema escrito de numerales árabes.

La primera máquina sumadora la inventó el matemático francés Blaise Pascal (1623-1662) a sus 18 años, en 1642. Era una maquina calculadora que podía sumar y restar.

El matemático alemán Gotfried Whilelm Leibniz (1646-1716) ideó una máquina calculadora en 1693, que superaba a la de Pascal. Mientras que esta ultima solo podía sumar y restar, la de Leibniz podía multiplicar por repetición automática de la suma, y dividir por repetición automática de la resta.

La primera calculadora electromecánica la invento el estadounidense Herman Hollerith (1860-1929), conocida como máquina tabuladora, la cual funcionaba con tarjetas perforadas.

Un gran salto en esta evolución fue la creación de la calculadora de bolsillo. En 1967, Jack Kilby, Jerry Merryman y James Van Tassel de Texas Instruments, desarrollaron la primera calculadora fácilmente transportable, llamada Datamath.

La primera calculadora capaz de realizar cálculos simbólicos fue la HP-28, lanzada en 1987. Era capaz, por ejemplo, de resolver simbólicamente ecuaciones cuadráticas. La primera calculadora gráfica fue la Casio fx7000G lanzada en 1985.

                                                -----à 

                                                                        

COMENTARIO:

El cálculo ha sido desde un principio muy importante para el ser humano, por eso para brindar mayor comodidad; matemáticos, científicos y otras personas inventaron la calculadora y a lo largo de los años han ido evolucionando rápidamente.

Este aparato, nos ayuda a resolver difíciles operaciones matemáticas con tan solo simples cálculos en segundos. Por otra parte, me impresiona que hayan evolucionado en gran cantidad, pues pasaron de una maquina que era 10 veces más grande y que no podía hacer mas cálculos que sumar y restar; a una de bolsillo, la cual puede hasta graficar.

Ana lucia Vargas Miranda. 4TO E-  N° 34

Formulas de esfera

Elementos de la esfera:

Circunferencias en la esfera:

Cálculo del radio de la esfera:

 

Calculamos la radio de la esfera, conociendo la distancia de un plano que corta la esfera y el radio de la sección, aplicando elteorema de Pitágoras en el triángulo sombreado:

 Área de la superficie esférica





Volumen de la esfera